| A170 |

# 1부터 100까지의 합 for 구문
sum = 0
for k in range(100) :
sum += (k+1)
print(sum)
| A171 |

# x의 n 제곱 for 구문
x=int(input('x= '))
n=int(input('n= '))
vp=1
for k in range(1,n+1):
vp *=x
print(vp)
| A172 |

# 반복문 중첩
for k in range(2,5):
for j in range(1,10):
print('%d x %d = %d' %(k,j,k*j))
print()
| A173 |

k=2
while k<=9:
j=1
while j<=9:
print('(%d x %d = %d)' %(k,j,k*j), end=" ")
j=j+1
k=k+1
print()

| 자리 확보를 통해 조금 더 깔끔(?) |

k=2
# j=1 # 이코드는 제대로 작동하지 않는다. ㅠㅜ
while k<=9:
j=1 # 이 위치에 초기화해야 하는 것 같다.
while j<=9:
# print('(%d x %d = %d)' %(k,j,k*j), end=" ")
print(f'({k} x {j} = {k*j})'.center(13), end=" ")
j=j+1
k=k+1
print()
| A174 |
 |
 |
# 소수 판단 프로그램
def primeNum(n) :
count = 0
namuji = 1
print("약수 : 1")
for i in range(2,n) :
namuji = n % i
if namuji == 0 :
count = count + 1
print("약수 : ",i)
if count == 0 :
print("약수 : %d" %(n))
print("%d는 소수입니다." %(n))
else :
print("약수 : %d" %(n))
print("합성수입니다.")
primeNum(37)
print()
primeNum(36)
print()
primeNum(49)
print()
primeNum(1) # 1에 대하여 기초수라는 출력은 코딩 안함
print()
n = input('수를 입력하세요. : ')
primeNum(int(n))
| A175 |

# 무한 반복문
# while과 True 이용!!
while True :
print("Forever")
# 정지는 Ctrl + C 또는 import창 닫기
| A176 |

# 알고리즘(algorithm)
# : 주어진 문제를 해결하기 위해 정해진 일련의 단계적 절차를 기술하는 것
# 플로우차트(flowchart) : 그림으로 데이터의 흐름을 나타냄
# 의사코드(pseudo code) : 프로그램 코드와 유사(블록코딩과 비슷한 듯)
| A177 |

# 반복문 안의 조건문
# 1부터 n까지의 m의 배수
print('1부터 n까지에서 m의 배수를 구하고자 합니다.')
n = int(input('n은? : '))
m = int(input('m은? : '))
print()
k = 1
p = 0
while k<=n :
if k % m == 0 :
print(k,end=(","))
p += 1
k += 1
print()
print("1부터 %d까지 %d의 배수는 총 %d개입니다." %(n,m,p))
| A178 |

# break문
n=10
while n >= -10 :
if n == 0 :
break # 0으로 나눌 수 없으니 break에
# 가장 가까운 반본문만 탈출
inv = 1.0 / n
print(inv)
n = n-2 # 감소폭 : 2
| A179 |
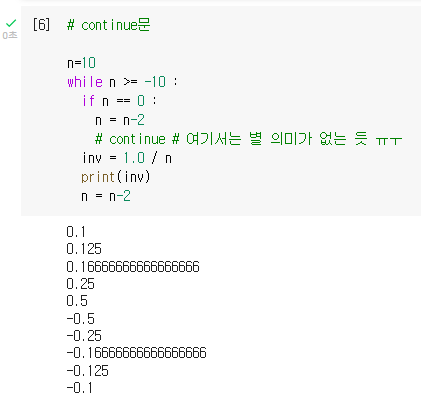
# continue문
n=10
while n >= -10 :
if n == 0 :
n = n-2
# continue # 여기서는 별 의미가 없는 듯 ㅠㅜ
inv = 1.0 / n
print(inv)
n = n-2
728x90

