728x90
뉴런과 퍼셉트론
1_SBlu465fze3Q9VGYjSbXow.png
0.26MB
출처 : https://medium.com/codex/the-mcculloch-pitts-ann-ba8c887769fc
출처 : https://www.youtube.com/watch?v=8Gpa_pdHrPE
| Dendrite : 이웃의 뉴런으로 부터 전기 신호를 받음 |
| ↓ |
| Synapse : 다른 뉴런과 Dendrite의 연결 부위에 위치 : 전기신호를 세기를 재조정함. |
| ↓ |
| Soma (cell body) : Dendrite로 부터 받은 여러개의 : 전기신호들을 모두 합침. |
| ↓ |
| Axon : Soma의 전위가 일정 이상이 되면 : 이웃의 뉴런으로 전기 신호를 보냄. |
| x₁ | w₁ | y |
| → | ||
| x₂ | → | |
| w₂ |
w1,w2 : 가중치 부여 (Synapse 역할)
:: 가중치 2이면 x2(증폭), 가중치가 0.5이면 x½(감축)
 |
| AND 게이트 |
| x₁ | x₂ | y | x₁ | x₂ | y | |
| True | True | True | 1 | 1 | 1 | |
| True | False | False | 1 | 0 | 0 | |
| False | True | False | 0 | 1 | 0 | |
| False | False | False | 0 | 0 | 0 |
| 전류가 흐른다 =1 =True 전류가 흐리지 않는다 =0 =False |
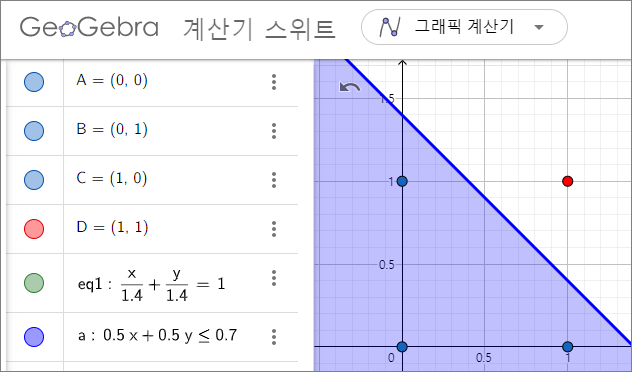
결정해야할 숫자는 3개 : w₁,w₂, 세타
w₁=0.5,
w₂=0.5,
세타=0.7
1*0.5+1*0.5=1 >0.7 결과 :1부여
1*0.5+0*0.5=0.5 <0.7 결과 :0부여
0*0.5+0*0.5=0 <0.7 결과 :0부여
AND 게이트 구현
| NAND 게이트 (Not AND 게이트) |
| x₁ | x₂ | y (not y) | x₁ | x₂ | y | |
| True | True | False | 1 | 1 | 0 | |
| True | False | True | 1 | 0 | 1 | |
| False | True | True | 0 | 1 | 1 | |
| False | False | True | 0 | 0 | 1 |
| 전류가 흐른다 =1 =True 전류가 흐리지 않는다 =0 =False |
결정해야할 숫자는 3개 : w₁,w₂, 세타
w₁=-0.5,
w₂=-0.5,
세타=-0.7
1*-0.5+1*-0.5=-1 <-0.7 결과 :0부여
1*-0.5+0*-0.5=-0.5 > -0.7 결과 :1부여
0*-0.5+0*-0.5=0 >-0.7 결과 :1부여
NAND 게이트 구현
| OR 게이트 |
| x₁ | x₂ | y (not y) | x₁ | x₂ | y | |
| True | True | True | 1 | 1 | 1 | |
| True | False | True | 1 | 0 | 1 | |
| False | True | True | 0 | 1 | 1 | |
| False | False | False | 0 | 0 | 0 |
| 전류가 흐른다 =1 =True 전류가 흐리지 않는다 =0 =False |
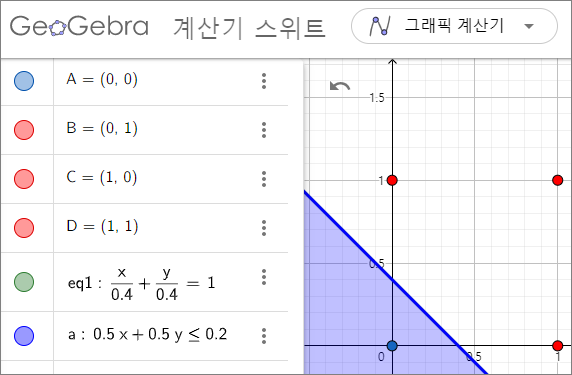
결정해야할 숫자는 3개 : w₁,w₂, 세타
w₁=0.5,
w₂=0.5,
세타=0.2
1*0.5+1*0.5=1 > 0.2 결과 :1부여
1*0.5+0*0.5=0.5 > 0.2 결과 :1부여
0*0.5+0*0.5=0 <0.2 결과 :2부여
OR 게이트 구현
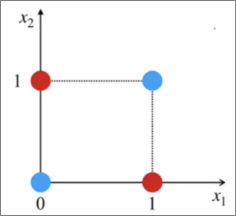
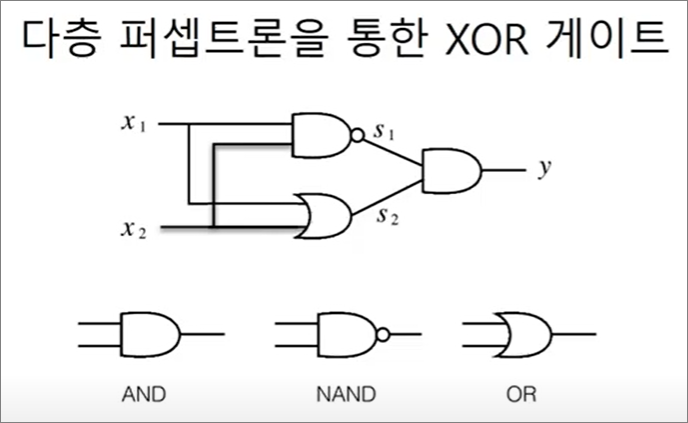
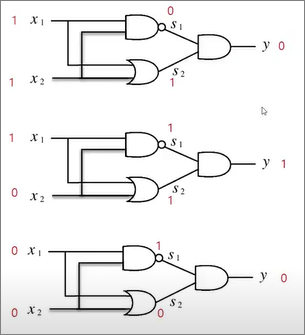
| XOR 게이트 (배타적 논리합) 다를 때만 True |
| x₁ | x₂ | y (not y) | x₁ | x₂ | y | |
| True | True | False | 1 | 1 | 0 | |
| True | False | True | 1 | 0 | 1 | |
| False | True | True | 0 | 1 | 1 | |
| False | False | False | 0 | 0 | 0 |
| 전류가 흐른다 =1 =True 전류가 흐리지 않는다 =0 =False |
결정해야할 숫자는 3개 : w₁,w₂, 세타
w₁=0.5,
w₂=0.5,
세타=0.2
명제
|
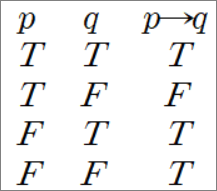
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
# AND GATE
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2]) # 벡터처럼 취급
w = np.array([0.5, 0.5]) # 리스트의 덧셈을
# 벡터의 덧셈처럼 편하게 계산할 수 있음
b = -0.7 # 쎄타 대신 바이어스(편향 bias)
# 우변의 쎄타를 좌변으로 이항
# 0.7 대신 -0.7이 됨.
tmp = np.sum(w*x)+b # 좌표별로 벡터처럼 곱셈
# x1*0.5+x2*0.5+(-0.7)
if tmp <=0:
return 0
else:
return 1
print('AND 게이트')
if __name__== '__main__':
for xs in [(0,0),(1,0),(0,1),(1,1)]:
y = AND(xs[0],xs[1])
print(str(xs) + " -> " + str(y))
|
cs |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
# NAND GATE
import numpy as np
def NAND(x1, x2):
x = np.array([x1, x2]) # 벡터처럼 취급
w = np.array([-0.5, -0.5]) # 리스트의 덧셈을
# 벡터의 덧셈처럼 편하게 계산할 수 있음
b = 0.7 # 쎄타 대신 바이어스(편향)
# 우변의 쎄타를 좌변으로 이항
# -0.7 대신 0.7이 됨.
tmp = np.sum(w*x)+b # 좌표별로 벡터처럼 곱셈
# x1*-0.5+x2*-0.5+0.7
if tmp <=0:
return 0
else:
return 1
print('NAND 게이트')
if __name__== '__main__':
for xs in [(0,0),(1,0),(0,1),(1,1)]:
y = NAND(xs[0],xs[1])
print(str(xs) + " -> " + str(y))
|
cs |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
# OR GATE
import numpy as np
def OR(x1, x2):
x = np.array([x1, x2]) # 벡터처럼 취급
w = np.array([0.5, 0.5]) # 리스트의 덧셈을
# 벡터의 덧셈처럼 편하게 계산할 수 있음
b = -0.2 # 쎄타 대신 바이어스(편향)
# 우변의 쎄타를 좌변으로 이항
# 0.2 대신 -0.2이 됨.
tmp = np.sum(w*x)+b # 좌표별로 벡터처럼 곱셈
# x1*0.5+x2*0.5+(-0.2)
if tmp <=0:
return 0
else:
return 1
print('OR 게이트')
if __name__== '__main__':
for xs in [(0,0),(1,0),(0,1),(1,1)]:
y = OR(xs[0],xs[1])
print(str(xs) + " -> " + str(y))
|
cs |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
import numpy as np
# AND GATE
def AND(x1, x2):
x = np.array([x1, x2]) # 벡터처럼 취급
w = np.array([0.5, 0.5]) # 리스트의 덧셈을
# 벡터의 덧셈처럼 편하게 계산할 수 있음
b = -0.7 # 쎄타 대신 바이어스(편향)
# 우변의 쎄타를 좌변으로 이항
# 0.7 대신 -0.7이 됨.
tmp = np.sum(w*x)+b # 좌표별로 벡터처럼 곱셈
# x1*0.5+x2*0.5+(-0.7)
if tmp <=0:
return 0
else:
return 1
# OR GATE
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w*x)+b
# x1*0.5+x2*0.5+(-0.2)
if tmp <=0:
return 0
else:
return 1
# NAND GATE
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w*x)+b
# x1*-0.5+x2*-0.5+0.7
if tmp <=0:
return 0
else:
return 1
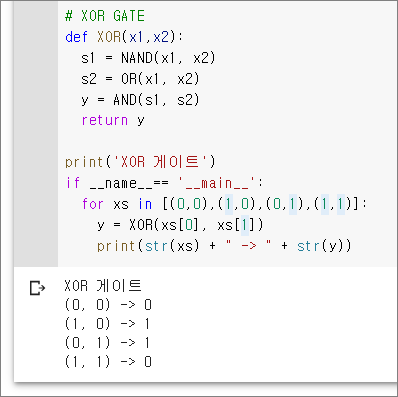
# XOR GATE
def XOR(x1,x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
print('XOR 게이트')
if __name__== '__main__':
for xs in [(0,0),(1,0),(0,1),(1,1)]:
y = XOR(xs[0], xs[1])
print(str(xs) + " -> " + str(y))
|
cs |
728x90