| 유리수의 가산 방법 |
유리수도 셀 수 있다?
HTML
https://zcrong01.github.io/math/Countable rational numbers_02.html
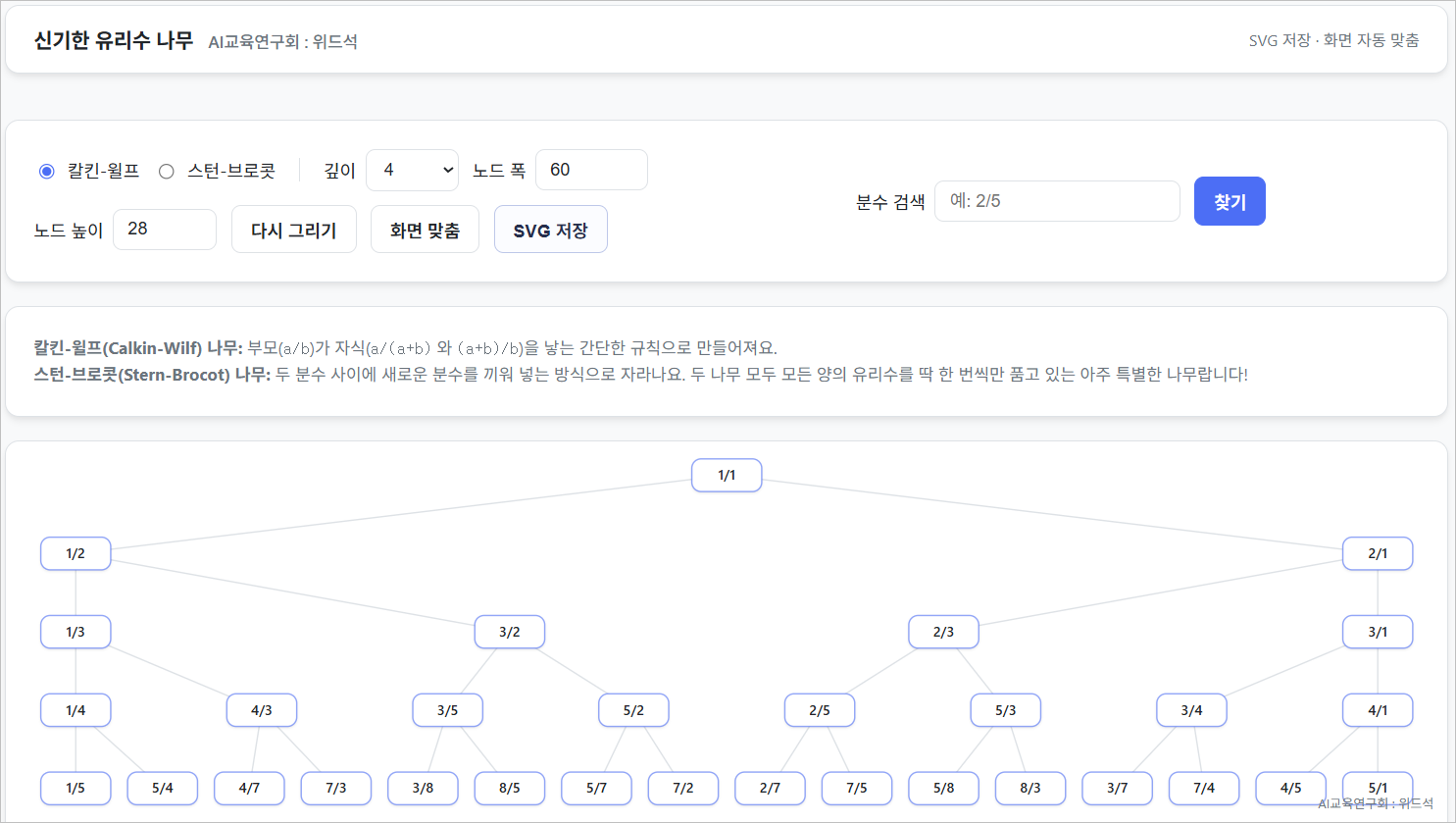
신기한 유리수 나무: Calkin–Wilf / Stern–Brocot 트리 시각화 (AI교육연구회 : 위드석)
신기한 유리수 나무 AI교육연구회 : 위드석 SVG 저장 · 화면 자동 맞춤
zcrong01.github.io
 |
유리수는 셀 수 있을까?
자연수 ℕ, 정수 ℤ, 유리수 ℚ, 실수 ℝ 중에서 유리수 ℚ가 가산(셀 수 있음, countable)이라는 사실은 직관적으로 이해하기 어렵습니다. 실수선 어디를 보아도 유리수가 “빽빽하게” 분포해 있는데, 어떻게 그것을 하나하나 자연수처럼 차례대로 셀 수 있을까요?
이를 증명하는 아름다운 방법으로 Calkin–Wilf 트리와 Stern–Brocot 트리가 있습니다. 두 가지 모두 유리수를 체계적으로, 중복 없이 나열해주며, 이를 통해 유리수가 자연수와 1:1 대응 가능함을 보여줍니다.
Calkin–Wilf 트리
Calkin–Wilf 트리는 다음과 같은 규칙으로 정의됩니다:
- 루트는
1/1. - 노드
a/b의 왼쪽 자식은a/(a+b), 오른쪽 자식은(a+b)/b.
이 과정을 반복하면 모든 양의 기약 유리수가 정확히 한 번씩 등장합니다.
즉, 깊이가 커질수록 유리수 전체를 빠짐없이 생성할 수 있습니다.
수학적 의미는 다음과 같습니다:
- 각 단계의 노드는 자연수 순서로 일렬 나열이 가능 → ℚ의 가산성 증명.
- 트리 구조를 따라가면, 유리수에 고유한 “주소”가 부여됩니다.
- 따라서 ℚ와 ℕ 사이의 전단사 함수(1:1 대응)가 명확히 구축됩니다.
Stern–Brocot 트리
Stern–Brocot 트리는 분수의 mediant 연산으로 구성됩니다:
- 좌우 경계
0/1과1/0에서 시작. - 두 분수
a/b와c/d의 중간 분수(=mediant)는(a+c)/(b+d). - 이 중간값을 삽입하며 계속 확장.
이 과정 역시 모든 양의 기약 유리수가 정확히 한 번씩 나타나며, 특히 Farey 수열 및 유리 근사와 밀접하게 연결됩니다.
수학적 의미는 다음과 같습니다:
- 유리수가 체계적 탐색으로 “빽빽하게” 구성됨을 시각적으로 확인 가능.
- 분수의 mediant는 기약분수 성질을 보장해 중복이 사라집니다.
- 따라서 Stern–Brocot 트리 역시 ℚ의 가산성을 보여주는 또 다른 강력한 도구입니다.
두 트리의 공통점과 차이
- 공통점: 모든 양의 기약 유리수를 중복 없이 생성, ℚ가 가산 집합임을 증명.
- 차이점:
- Calkin–Wilf: 부모→자식 규칙, 단순 재귀 구조.
- Stern–Brocot: mediant 삽입, 분수 사이의 관계 강조.
유리수 가산성의 수학적 의미
이 두 가지 트리는 단순히 “유리수를 나열할 수 있다”는 사실을 넘어서,
무한 집합의 크기를 비교하는 칸토어의 이론과 직결됩니다.
- 자연수와 유리수는 서로 다른 집합이지만, 농도(기수)는 같습니다: ℵ₀.
- 즉, “조밀하게 분포”한다고 해서 “더 큰 크기의 무한”은 아님.
- 반대로, 실수 집합은 비가산임이 대각선 논법으로 드러납니다 → 유리수와의 근본적 차이.
정리
- Calkin–Wilf 트리와 Stern–Brocot 트리는 유리수 전체를 중복 없이 생성하는 체계적인 방법입니다.
- 이를 통해 유리수가 가산 무한집합임이 직관적으로 드러납니다.
- 칸토어가 보여준 무한 집합의 위계 속에서, 유리수는 자연수와 같은 크기(ℵ₀)라는 점이 명확해집니다.
'ㅡ■ work-Math' 카테고리의 다른 글
| 원소 주기율표:반응형 (HTML) (0) | 2025.08.23 |
|---|---|
| 로또 확률 체험 15C3 조합 [HTML] (1) | 2025.08.09 |
| 삼각함수 그래프 abcd [HTML,xls] (0) | 2025.08.09 |
| 에라토스테네스의 체 [HTML / exe / xls] (0) | 2025.06.15 |
| 에라토스네테스의 체 [xls,vba] (1) | 2024.03.08 |
